| Lantos Attila | Dudás András | Répási Zoltán | Vígh Imre |
| csapatvezető | csapattitkár | oktató | csapat koordinátor |
| 70/775-2613 | 30/844-5173 | 70/367-8411 | 30/768-6742 |
| lantosati@gmail.hu | repa1003@freemail.hu | vighim@gmail.com |
Archívum a ‘’ Kategóriában
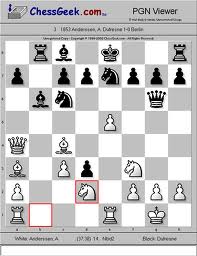
A nyolckirálynő-probléma egy sakkfeladvány, lényege a következő: hogyan lehet 8 királynőt úgy elhelyezni egy 8×8-as sakktáblán, hogy a sakk szabályai szerint ne üssék egymást. Ehhez a királynő/vezér lépési lehetőségeinek ismeretében az kell, hogy ne legyen két bábu azonos sorban, oszlopban vagy átlóban.
A nyolckirálynő-probléma egy példa az ennél általánosabb „n királynő problémára”, ami azt a kérdést veti fel, hányféleképpen lehet lerakni n darab királynőt egy n×n-es táblán.
Történet:
A kérdést először Max Bezzel vetette fel 1848-ban. Az évek során sok matematikus – többek között Gauss és Georg Cantor – foglalkozott vele, és az általánosított n-királynő-problémával.
Az első megoldást Franz Nauck adta 1850-ben.
1874-ben S. Gunther determinánsok használatával adott egy eljárást, amivel lerakhatóak a bábuk. Később ezt J. W. L. Glaisher finomította.
Edsger Dijkstra 1972-ben arra használta ezt a problémát, hogy bemutassa a strukturált programozás előnyeit, erejét. Publikált egy részletes leírást a backtrack algoritmusról.
Megoldás:
A megoldás nehezen számítható ki, mivel a bábuknak összesen ![]() különböző lerakása létezik, de ebből csak 92 felel meg az n-királynő probléma szabályainak. Ez igen nagy számítási időt jelent. Az összes lehetséges lerakások száma, és ezáltal a számításhoz szükséges idő csökkenthető azáltal, hogy bevezetünk egy olyan szabályt, miszerint minden sorban (vagy oszlopban) csak egy-egy bábu állhat. Így a vizsgálandó lerakások száma csupán
különböző lerakása létezik, de ebből csak 92 felel meg az n-királynő probléma szabályainak. Ez igen nagy számítási időt jelent. Az összes lehetséges lerakások száma, és ezáltal a számításhoz szükséges idő csökkenthető azáltal, hogy bevezetünk egy olyan szabályt, miszerint minden sorban (vagy oszlopban) csak egy-egy bábu állhat. Így a vizsgálandó lerakások száma csupán ![]() (16884-szer kevesebb). Ez n=8-ra kezelhető, de megengedhetetlenül nagy például n=1 000 000-ra már nem.
(16884-szer kevesebb). Ez n=8-ra kezelhető, de megengedhetetlenül nagy például n=1 000 000-ra már nem.
Algoritmizálási szempontból a bábuk helyét érdemes tömbként kezelni: mivel minden sorban csak egyetlen bábu állhat, ezért elég a sorokat megszámozni (1-től n-ig), majd n darab számot lejegyezni aszerint, hogy az n-edik sorban hányadik helyen áll bábu.
Itt egy algoritmus, ami egy – a probléma szabályainak megfelelő – tömböt ad eredményül (n≥4 és n=1 esetekre):
- Osszuk el n-et 12-vel. Jegyezzük le a maradékot.
- Írjuk le egy listába 2-től n-ig a páros számokat növekvő sorrendben.
- Ha a maradék 3 vagy 9, akkor a 2-es számot vigyük át a lista végére.
- Írjuk a lista végére 1-től n-ig a páratlan számokat növekvő sorrentben, de ha a maradék 8, akkor páronként cseréljük fel őket (például 3, 1, 7, 5, 11, 9, …).
- Ha a maradék 2, akkor cseréljük ki az 1-et és 3-at, valamint tegyük az 5-öt a lista végére.
- Ha a maradék 3 vagy 9, akkor tegyük az 1-et és 3-at a lista végére (ebben a sorrendben).
Végül tegyük le a bábukat a sakktáblára: az első sorba oda, ahova a lista első száma mutatja; a második sorba oda, ahová a lista második száma mutatja…
Néhány példa:
- 14 királynő: 2, 4, 6, 8, 10, 12, 14, 3, 1, 7, 9, 11, 13, 5
- 15 királynő: 4, 6, 8, 10, 12, 14, 2, 5, 7, 9, 11, 13, 15, 1, 3
- 20 királynő: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 3, 1, 7, 5, 11, 9, 15, 13, 19, 17
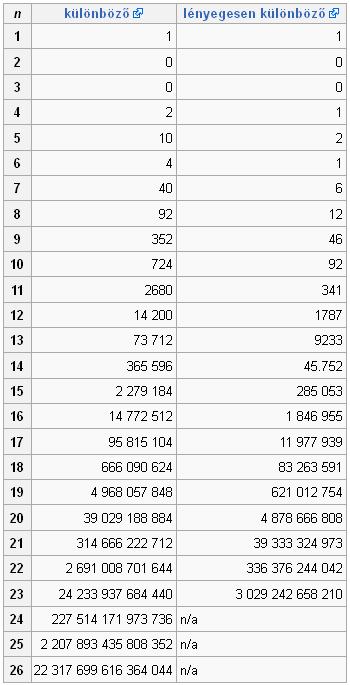
A probléma megoldásainak száma (n≤26)
Az alábbi táblázat tartalmazza a lerakások számát. A lényegesen különböző oszlopban jegyzett értékeket úgy kaptuk, hogy az elforgatással vagy tükrözéssel egymásba vihető lerakásokat csak egyszer számoltuk meg.
A probléma megoldásai n=8 esetben
Mint a fenti táblázat mutatja, egy szabványos, 8×8-as táblán 92 olyan lerakási mód van, amikor a királynők nem ütik egymást. Az elforgatással nem egymásba vihetőek alább láthatóak:
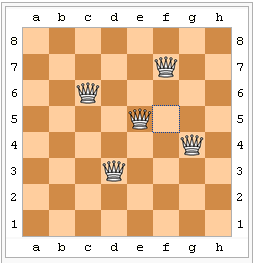
Adott egy n×n-es sakktábla (ahol n pozitív egész). Szeretnénk úgy királynőket elhelyezni a táblán, hogy bárhova is tennénk új bábut, az már valamelyik korábbi királynő által ütésben legyen. Keressük a királynők minimális számát.
Megoldás:
A probléma az alkalmazott diszkrét matematika témakörébe tartozik. Egyelőre nincs egzakt eredmény, amellyel tetszőleges n értékére kiszámítható lenne a szükséges királynők száma. A királynők minimális számára azonban már született felső becslés. Kis n értékekre számítógéppel kipróbálható valamennyi szóba jöhető állás, és így megkapható a kérdéses szám.
Az alábbi táblázat mutatja a különböző méretű sakktáblákhoz tartozó domináns királynők számát:
| A tábla mérete | Domináns királynők |
| 1×1 | 1 |
| 2×2 | 1 |
| 3×3 | 1 |
| 4×4 | 3 |
| 5×5 | 3 |
| 6×6 | 4 |
| 7×7 | 4 |
| 8×8 | 5 |
| 9×9 | 5 |
| 10×10 | 5 |
| 11×11 | 5 |
| 12×12 | 7 |
| 13×13 | 7 |
| 14×14 | 8 |
| 15×15 | 9 |
| 16×16 | 9 |
| 17×17 | 9 |
| 18×18 | 10 |
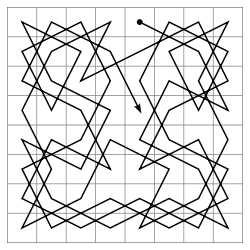
Matematikai problémákat is fel lehet vetni a sakktáblán. Ilyen például a domináns királynők problémája vagy a nyolckirálynő-probléma. De olyan feladványok is lázban tartották az embereket, mint például végig lehet-e egy huszárral úgy menni mind a 64 mezőn, hogy egy mezőre csak egyszer léphet rá. Ez a feladat huszárvándorlás-probléma néven vált ismertté. Az utóbbi feladatra jobb oldalon található egy lehetséges megoldás.

Möbius-szalag
A szalagot könnyen elkészíthetjük egy papírcsíkból, ha végeit összeragasztjuk úgy, hogy az egyiket 180°-kal elfordítjuk. Az egyoldalúságról úgy győződhetünk meg, ha egy ceruzával hosszirányban a közepén csíkot húzunk, visszajutunk oda, ahonnan elindultunk, bejárva az eredeti fizikai szalag mindkét oldalát. További érdekesség, hogy ha kettévágjuk az imént említett vonal mentén, egy, az eredeti szalagnál kétszer hosszabb (fele olyan széles), immár kétoldalú felületet kapunk. Ha még egyszer hasonló módon körbevágjuk, akkor két egymásba fonódó szalag lesz az eredmény. Ha három részre vágjuk, akkor két egymásba fonódó szalagot kapunk: az egyik újra Möbius-szalag, a másik egy kétszer olyan hosszú szalag, ami kétszer csavart.
A hasonlóan páratlan számszor csavart szalagok darabolása hasonló érdekes eredményt ad. Például a háromszor 180 fokosan csavarodó szalag kettévágásával lóherecsomót kapunk. A végeredményként kapott csavarodások száma kiszámítható a következő egyenletből: 2N + 2 = M, ahol N a csavarodások eredeti száma, és M a csavarodások kapott száma. A Möbius-szalaghoz hasonlóan a páratlan számszor csavart szalagoknak egy élük és egy oldaluk van. A páros számszor csavartak ellenben két oldalúak és két élűek.

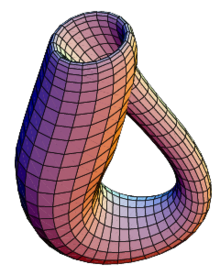
A Klein-palack.
Egy hasonlóan furcsa objektum a Klein-palack. Ez megkapható két Möbius-szalagból a két szalag éleinek azonosításával. A Klein-palack nem ágyazható be a három dimenziós euklidészi térbe önátmetszés nélkül. A Klein-féle palack egy kétdimenziós, egyoldalú (vagyis nem irányítható) felület, önmagába forduló rugalmas kúpként lehet elképzelni. A palacknak a belseje egyben a külseje is, tehát ha a felületét elkezdenénk festeni, az ecset felemelése nélkül ki tudnánk festeni az egészet. Nevét Felix Klein német matematikusról kapta.